アキレスがカメに云ったこと [ノート]
前にアキレスとカメのパラドクスについてちょっと書いたが、その後ルイス・キャロルのアキレスとカメのことが気になりだして、初めてその What the Tortoise Said to Achilles (1895) に眼を通してみたところ、これがどうもいまひとつ腑に落ちないのだった。ドジソンではなくキャロルの名で書かれているだけあって、何やらワンダーランドめいているとでも云おうか。そこで、以下にその核心部を余計なおしゃべりを適宜省略しつつ引いて、少しばかりコメントを付しておこうと思う――あいかわらず他に書きたいことも無いので。
ACHILLES had overtaken the Tortoise, and had seated himself comfortably on its back.
"So you've got to the end of our race-course?" said the Tortoise. "Even though it does consist of an infinite series of distances? I thought some wiseacre or other had proved that the thing couldn't be done?"
"It can be done," said Achilles. "It has been done! Solvitur ambulando. You see the distances were constantly diminishing; and so—"
"But if they had been constantly increasing?" the Tortoise interrupted...
"... Well now, would you like to hear of a race-course, that most people fancy they can get to the end of in two or three steps, while it really consists of an infinite number of distances, each one longer than the previous one?"
"Very much indeed!" said the Grecian warrior, as he drew from his helmet ... an enormous note-book and a pencil. "Proceed! And speak slowly, please! Short-hand isn't invented yet!"
... "Well, now, let's take a little bit of the argument in that First Proposition [of Euclid]—just two steps, and the conclusion drawn from them. Kindly enter them in your note-book. And in order to refer to them conveniently, let's call them A, B, and Z:—
(A) Things that are equal to the same are equal to each other.
(B) The two sides of this Triangle are things that are equal to the same.
(Z) The two sides of this Triangle are equal to each other.
Readers of Euclid will grant, I suppose, that Z follows logically from A and B, so that any one who accepts A and B as true, must accept Z as true?"
"Undoubtedly! The youngest child in a High School ... will grant that."
"And if some reader had not yet accepted A and B as true, he might still accept the sequence as a valid one, I suppose?"
"No doubt such a reader might exist. He might say 'I accept as true the Hypothetical Proposition that, if A and B be true, Z must be true; but, I don't accept A and B as true.' Such a reader would do wisely in abandoning Euclid, and taking to football."
"And might there not also be some reader who would say 'I accept A and B as true, but I don't accept the Hypothetical'?"
"Certainly there might. He, also, had better take to football."
"And neither of these readers," the Tortoise continued, "is as yet under any logical necessity to accept Z as true?"
"Quite so," Achilles assented.
"Well, now, I want you to consider me as a reader of the second kind, and to force me, logically, to accept Z as true."
... "I'm to force you to accept Z, am I?" Achilles said musingly. "And your present position is that you accept A and B, but you don't accept the Hypothetical—"
"Let's call it C," said the Tortoise.
"—but you don't accept
(C) If A and B are true, Z must be true."
"That is my present position," said the Tortoise.
"Then I must ask you to accept C."
"I'll do so," said the Tortoise, "as soon as you've entered it in that note-book of yours. What else have you got in it?"
"Only a few memoranda," said Achilles, nervously fluttering the leaves: "a few memoranda of—of the battles in which I have distinguished myself!"
"Plenty of blank leaves, I see!" the Tortoise cheerily remarked. "We shall need them all!" (Achilles shuddered.) "Now write as I dictate:—
(A) Things that are equal to the same are equal to each other.
(B) The two sides of this Triangle are things that are equal to the same.
(C) If A and B are true, Z must be true.
(Z) The two sides of this Triangle are equal to each other."
"You should call it D, not Z," said Achilles. "It comes next to the other three. If you accept A and B and C, you must accept Z."
"And why must I?"
"Because it follows logically from them. If A and B and C are true, Z must be true. You don't dispute that, I imagine?"
"If A and B and C are true, Z must be true," the Tortoise thoughtfully repeated. "That's another Hypothetical, isn't it? And, if I failed to see its truth, I might accept A and B and C, and still not accept Z, mightn't I?”
"You might," the candid hero admitted; "though such obtuseness would certainly be phenomenal. Still, the event is possible. So I must ask you to grant one more Hypothetical."
"Very good. I'm quite willing to grant it, as soon as you've written it down..."...
まず注意しておきたいのは、これが論理学と数学がモダナイズされようとしていた時代のさなかに書かれたもので、いわゆる伝統的論理学とユークリッド原論の初歩の知識を前提としている、ということだ。（問題の推論は、形はやや異なるものの、実際にユークリッド原論第一巻の第一命題の証明中に見出せる。その命題は、所与の直線をもとに等辺三角形を構成すること、というもので、その証明は下の図のように円の性質に依拠している。（the two sides of this Triangle というのは ΑΓ と ΒΓ のことだ。）なお、ユークリッドにおいては線はもっぱら有限だ。）仮令ユークリッドの読者の誰かが A と B を真だと認めなかったとしても、それでもやはり彼は A と B から Z に到るシークエンスを妥当なものと認めることだろう、というカメの言葉に同意したあとで、アキレスがさらに、そのような者は「私は、A と B が真ならば Z は真であるほかない、という仮言命題を真だと認めるが、A と B を真だとは認めない」と云うことだろう、とわざわざ付け加えるのは、それがこのような場合に論理学の心得があることを示すためにひとが口にすべき紋切型というやつだから、という訳なのだろう。アキレスは、どうやら、「do not accept as true」を、理解できなくて真だと受け容れることができない、というほどの意味に解して、論理学の初歩を一応は知っているもののユークリッド入門に躓いた少年を想い描いているようだ。（ユークリッドの初歩を理解できないような少年でも問題の推論は妥当だとちゃんと判断できる、という想定はさほど不自然なものではないかも知れない。件の推論はいわゆる定言三段論法の第一格 AAA（通称 Barbara）という妥当な推論の典型中の典型に収まるものと看做し得るからだ。なお、定言三段論法の妥当性は、前提が何れも真ならば結論は真であるほかない、ということによって規定される。）ここまではまあいいとしよう。ところが、その紋切型を待ってましたとばかりに、カメが、それなら「私は A と B を真だと認めるが、件の仮言を認めない」と云う者だっているのではないか、とたたみかけ、アキレスがそれをあっさりと肯定してしまうところから話がおかしくなる。
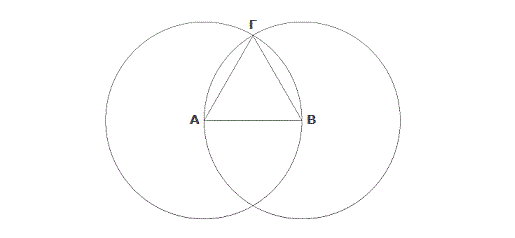ここでまず気になるのはそのような者は何を根拠に B を真だと認めるのか――A はユークリッドの第一公理だからそのまま真だと認めていいにしても――ということだ。B を云うには直線 ΑΓ と ΒΓ がそれぞれに ΑΒ に等しいことを示せば足りる訳だが、第一命題の証明には、簡略に、点 Α は左側の円の中心だから ΑΓ は ΑΒ に等しい、というような意味のことしか述べられていないので、それを敷衍してみれば、以下のようになるだろう。
まず、Heath による英訳から円とその中心の定義（第十五および第十六定義）を引けば次の通り：
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
16. And the point is called the centre of the circle.
ここから次のような命題が得られるだろう：
All the straight lines falling upon the circumscribing line of a circle from its centre are equal to one another.
一方、ΑΒ と ΑΓ については次が得られる：
ΑΒ and ΑΓ are straight lines that are falling upon the circumscribing line of a circle from its centre.
これらから次が帰結する：
ΑΒ and ΑΓ are equal to one another.
これは、だが、問題の推論と同型の三段論法だ。件の仮言命題を認めないという彼奴はこれに係わる同様の仮言を認めるのか認めないのか？ アキレスはそう問うてみてもよかったかも知れない。
もっとも、俺が解せないのはこの点ではない。問題はこれからだ。アキレスは「私を第二の類の読者だと想定して、Z を真だと論理的に認めざるを得ないようにしてみてほしい」というカメの誘いにこれまたあっさりと乗って、カメの仮想上の立場を確認したうえで「そこで俺はお前に C を認めて貰わねばならない訳だ」とこれまたわざわざ付け加え、そしてこれまたそれを待ってましたとばかりにカメが返した「そうしよう。それをそのノートに書込んでくれさえすれば」という言葉にまたまたあっさりと応じてしまう。そもそもカメが成り代わっている人物は C を認めないはずだったのに、しかもアキレスとカメはそれを確認したばかりなのに、いったいこれはどうしたことなのか？ アキレスはカメと一丸となってもっぱら C の類の仮言命題を再帰的に弾き出し続けるマシーンと化すことをひたすら望んでいるかの如くだ。やはり彼らは追いかけっこするうちにいつのまにかワンダーランドに迷い込んでしまったものに相違ない。
ところで、この理不尽な展開を補うべく、アキレスは C を受け容れさせることでカメの論理学的無知を埋めようとし、カメはそれを甘受する、といった脚色がなされたりすることがあるが、もちろん、そうしたストーリーは他にも色々と考えてみることができる。そして、それにつれて例えば次のような一聯の問いが浮かびあがって来る： A と B が真ならば Z は真であるほかないという命題を真だと認めることと A と B が真ならば Z は真であるほかないということを認めることは同じではないだろうが、ならばそれらはどう違うのか？ そもそも A と B が真ならば Z は真であるほかないという命題を真だと認めるとはどういうことなのか？ ひとがそれをそう認めているということのクリテリオンは何なのか？ A と B が真ならば Z は真であるほかないということを認めるとはどういうことなのか？ ひとがそれを認めているということのクリテリオンは何なのか？・・・ ひょっとして、キャロルはこうした効果を狙って、敢えて無造作な語り方を選んだのでもあろうか。ちなみに、カメは最後の方で「what a lot of instruction this colloquy of ours will provide for the Logicians of the Nineteenth Century」と云っているが、どうやらこの対話篇には、様々なインストラクションやインスピレーションを提供すべく、あれこれ仕掛けが施されているらしい。やはりキャロルの名義は伊達ではないようだ。（ついでに、このあとの展開を書いておけば、透明だった語り手が見物していた第三者として顕われて、彼は銀行に急用があったのでその場を離れねばならず、数箇月後にふたたび通りかかってみると、一千一箇目の仮言命題をアキレスが書き終えたところだった、ということになっている。だが、そう語っているのは最初の語り手なのか、それとも第二の透明な語り手なのか？）
それはそうと、カメが成り代わっている人物は A と B を真だと認めるが C を認めない者としかされていないのだから、彼に代わって云い得ることは実は何も無い。可能なのは、ただ、何か妥当な推論が呈示されるたびに、それに係わる C と同様の仮言命題を彼はやはり認めないかも知れない、と指摘することだけだろう。そこで、彼が演繹的推論を悉く受けつけない推論盲とでも呼び得るような者だったとしたら、と考えてみたくなるのは俺ばかりではあるまい。ヴィトゲンシュタインは『哲学探求』第二部で、例えばウサギ‐アヒルの図を兎として見たり家鴨として見たりすることができないような者を想定し、アスペクト盲と呼んで「概念的診察」をおこなっているが、それに倣って、推論盲の概念的診察を試みればどういうことになるか。とっくに誰かがやっているだろうか？
最後に問題の推論を量化理論に拠ってパラフレーズしておく。
(A') ∀x∀y(∃z((x is equal to z)∧(y is equal to z))⊃(x and y are equal to each other))
これから普遍例化によって次が得られる：
(A'') ∃z((ΑΓ is equal to z)∧(ΒΓ is equal to z))⊃(ΑΓ and ΒΓ are equal to each other)
これと
(B') ∃z((ΑΓ is equal to z)∧(ΒΓ is equal to z))
から、モドゥス・ポネンスによって次が得られる：
(Z') (ΑΓ and ΒΓ are equal to each other)
A' が真ならば当然 A'' も真だが、さらに B' が真だとすれば Z' が真であるほかないことは A'' の形から一目瞭然だ。もちろん、C を認めない彼奴はこれもまた認めないかも知れないが。
ACHILLES had overtaken the Tortoise, and had seated himself comfortably on its back.
"So you've got to the end of our race-course?" said the Tortoise. "Even though it does consist of an infinite series of distances? I thought some wiseacre or other had proved that the thing couldn't be done?"
"It can be done," said Achilles. "It has been done! Solvitur ambulando. You see the distances were constantly diminishing; and so—"
"But if they had been constantly increasing?" the Tortoise interrupted...
"... Well now, would you like to hear of a race-course, that most people fancy they can get to the end of in two or three steps, while it really consists of an infinite number of distances, each one longer than the previous one?"
"Very much indeed!" said the Grecian warrior, as he drew from his helmet ... an enormous note-book and a pencil. "Proceed! And speak slowly, please! Short-hand isn't invented yet!"
... "Well, now, let's take a little bit of the argument in that First Proposition [of Euclid]—just two steps, and the conclusion drawn from them. Kindly enter them in your note-book. And in order to refer to them conveniently, let's call them A, B, and Z:—
(A) Things that are equal to the same are equal to each other.
(B) The two sides of this Triangle are things that are equal to the same.
(Z) The two sides of this Triangle are equal to each other.
Readers of Euclid will grant, I suppose, that Z follows logically from A and B, so that any one who accepts A and B as true, must accept Z as true?"
"Undoubtedly! The youngest child in a High School ... will grant that."
"And if some reader had not yet accepted A and B as true, he might still accept the sequence as a valid one, I suppose?"
"No doubt such a reader might exist. He might say 'I accept as true the Hypothetical Proposition that, if A and B be true, Z must be true; but, I don't accept A and B as true.' Such a reader would do wisely in abandoning Euclid, and taking to football."
"And might there not also be some reader who would say 'I accept A and B as true, but I don't accept the Hypothetical'?"
"Certainly there might. He, also, had better take to football."
"And neither of these readers," the Tortoise continued, "is as yet under any logical necessity to accept Z as true?"
"Quite so," Achilles assented.
"Well, now, I want you to consider me as a reader of the second kind, and to force me, logically, to accept Z as true."
... "I'm to force you to accept Z, am I?" Achilles said musingly. "And your present position is that you accept A and B, but you don't accept the Hypothetical—"
"Let's call it C," said the Tortoise.
"—but you don't accept
(C) If A and B are true, Z must be true."
"That is my present position," said the Tortoise.
"Then I must ask you to accept C."
"I'll do so," said the Tortoise, "as soon as you've entered it in that note-book of yours. What else have you got in it?"
"Only a few memoranda," said Achilles, nervously fluttering the leaves: "a few memoranda of—of the battles in which I have distinguished myself!"
"Plenty of blank leaves, I see!" the Tortoise cheerily remarked. "We shall need them all!" (Achilles shuddered.) "Now write as I dictate:—
(A) Things that are equal to the same are equal to each other.
(B) The two sides of this Triangle are things that are equal to the same.
(C) If A and B are true, Z must be true.
(Z) The two sides of this Triangle are equal to each other."
"You should call it D, not Z," said Achilles. "It comes next to the other three. If you accept A and B and C, you must accept Z."
"And why must I?"
"Because it follows logically from them. If A and B and C are true, Z must be true. You don't dispute that, I imagine?"
"If A and B and C are true, Z must be true," the Tortoise thoughtfully repeated. "That's another Hypothetical, isn't it? And, if I failed to see its truth, I might accept A and B and C, and still not accept Z, mightn't I?”
"You might," the candid hero admitted; "though such obtuseness would certainly be phenomenal. Still, the event is possible. So I must ask you to grant one more Hypothetical."
"Very good. I'm quite willing to grant it, as soon as you've written it down..."...
まず注意しておきたいのは、これが論理学と数学がモダナイズされようとしていた時代のさなかに書かれたもので、いわゆる伝統的論理学とユークリッド原論の初歩の知識を前提としている、ということだ。（問題の推論は、形はやや異なるものの、実際にユークリッド原論第一巻の第一命題の証明中に見出せる。その命題は、所与の直線をもとに等辺三角形を構成すること、というもので、その証明は下の図のように円の性質に依拠している。（the two sides of this Triangle というのは ΑΓ と ΒΓ のことだ。）なお、ユークリッドにおいては線はもっぱら有限だ。）仮令ユークリッドの読者の誰かが A と B を真だと認めなかったとしても、それでもやはり彼は A と B から Z に到るシークエンスを妥当なものと認めることだろう、というカメの言葉に同意したあとで、アキレスがさらに、そのような者は「私は、A と B が真ならば Z は真であるほかない、という仮言命題を真だと認めるが、A と B を真だとは認めない」と云うことだろう、とわざわざ付け加えるのは、それがこのような場合に論理学の心得があることを示すためにひとが口にすべき紋切型というやつだから、という訳なのだろう。アキレスは、どうやら、「do not accept as true」を、理解できなくて真だと受け容れることができない、というほどの意味に解して、論理学の初歩を一応は知っているもののユークリッド入門に躓いた少年を想い描いているようだ。（ユークリッドの初歩を理解できないような少年でも問題の推論は妥当だとちゃんと判断できる、という想定はさほど不自然なものではないかも知れない。件の推論はいわゆる定言三段論法の第一格 AAA（通称 Barbara）という妥当な推論の典型中の典型に収まるものと看做し得るからだ。なお、定言三段論法の妥当性は、前提が何れも真ならば結論は真であるほかない、ということによって規定される。）ここまではまあいいとしよう。ところが、その紋切型を待ってましたとばかりに、カメが、それなら「私は A と B を真だと認めるが、件の仮言を認めない」と云う者だっているのではないか、とたたみかけ、アキレスがそれをあっさりと肯定してしまうところから話がおかしくなる。
まず、Heath による英訳から円とその中心の定義（第十五および第十六定義）を引けば次の通り：
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
16. And the point is called the centre of the circle.
ここから次のような命題が得られるだろう：
All the straight lines falling upon the circumscribing line of a circle from its centre are equal to one another.
一方、ΑΒ と ΑΓ については次が得られる：
ΑΒ and ΑΓ are straight lines that are falling upon the circumscribing line of a circle from its centre.
これらから次が帰結する：
ΑΒ and ΑΓ are equal to one another.
これは、だが、問題の推論と同型の三段論法だ。件の仮言命題を認めないという彼奴はこれに係わる同様の仮言を認めるのか認めないのか？ アキレスはそう問うてみてもよかったかも知れない。
もっとも、俺が解せないのはこの点ではない。問題はこれからだ。アキレスは「私を第二の類の読者だと想定して、Z を真だと論理的に認めざるを得ないようにしてみてほしい」というカメの誘いにこれまたあっさりと乗って、カメの仮想上の立場を確認したうえで「そこで俺はお前に C を認めて貰わねばならない訳だ」とこれまたわざわざ付け加え、そしてこれまたそれを待ってましたとばかりにカメが返した「そうしよう。それをそのノートに書込んでくれさえすれば」という言葉にまたまたあっさりと応じてしまう。そもそもカメが成り代わっている人物は C を認めないはずだったのに、しかもアキレスとカメはそれを確認したばかりなのに、いったいこれはどうしたことなのか？ アキレスはカメと一丸となってもっぱら C の類の仮言命題を再帰的に弾き出し続けるマシーンと化すことをひたすら望んでいるかの如くだ。やはり彼らは追いかけっこするうちにいつのまにかワンダーランドに迷い込んでしまったものに相違ない。
ところで、この理不尽な展開を補うべく、アキレスは C を受け容れさせることでカメの論理学的無知を埋めようとし、カメはそれを甘受する、といった脚色がなされたりすることがあるが、もちろん、そうしたストーリーは他にも色々と考えてみることができる。そして、それにつれて例えば次のような一聯の問いが浮かびあがって来る： A と B が真ならば Z は真であるほかないという命題を真だと認めることと A と B が真ならば Z は真であるほかないということを認めることは同じではないだろうが、ならばそれらはどう違うのか？ そもそも A と B が真ならば Z は真であるほかないという命題を真だと認めるとはどういうことなのか？ ひとがそれをそう認めているということのクリテリオンは何なのか？ A と B が真ならば Z は真であるほかないということを認めるとはどういうことなのか？ ひとがそれを認めているということのクリテリオンは何なのか？・・・ ひょっとして、キャロルはこうした効果を狙って、敢えて無造作な語り方を選んだのでもあろうか。ちなみに、カメは最後の方で「what a lot of instruction this colloquy of ours will provide for the Logicians of the Nineteenth Century」と云っているが、どうやらこの対話篇には、様々なインストラクションやインスピレーションを提供すべく、あれこれ仕掛けが施されているらしい。やはりキャロルの名義は伊達ではないようだ。（ついでに、このあとの展開を書いておけば、透明だった語り手が見物していた第三者として顕われて、彼は銀行に急用があったのでその場を離れねばならず、数箇月後にふたたび通りかかってみると、一千一箇目の仮言命題をアキレスが書き終えたところだった、ということになっている。だが、そう語っているのは最初の語り手なのか、それとも第二の透明な語り手なのか？）
それはそうと、カメが成り代わっている人物は A と B を真だと認めるが C を認めない者としかされていないのだから、彼に代わって云い得ることは実は何も無い。可能なのは、ただ、何か妥当な推論が呈示されるたびに、それに係わる C と同様の仮言命題を彼はやはり認めないかも知れない、と指摘することだけだろう。そこで、彼が演繹的推論を悉く受けつけない推論盲とでも呼び得るような者だったとしたら、と考えてみたくなるのは俺ばかりではあるまい。ヴィトゲンシュタインは『哲学探求』第二部で、例えばウサギ‐アヒルの図を兎として見たり家鴨として見たりすることができないような者を想定し、アスペクト盲と呼んで「概念的診察」をおこなっているが、それに倣って、推論盲の概念的診察を試みればどういうことになるか。とっくに誰かがやっているだろうか？
最後に問題の推論を量化理論に拠ってパラフレーズしておく。
(A') ∀x∀y(∃z((x is equal to z)∧(y is equal to z))⊃(x and y are equal to each other))
これから普遍例化によって次が得られる：
(A'') ∃z((ΑΓ is equal to z)∧(ΒΓ is equal to z))⊃(ΑΓ and ΒΓ are equal to each other)
これと
(B') ∃z((ΑΓ is equal to z)∧(ΒΓ is equal to z))
から、モドゥス・ポネンスによって次が得られる：
(Z') (ΑΓ and ΒΓ are equal to each other)
A' が真ならば当然 A'' も真だが、さらに B' が真だとすれば Z' が真であるほかないことは A'' の形から一目瞭然だ。もちろん、C を認めない彼奴はこれもまた認めないかも知れないが。
2015-03-17 11:59
コメント(0)
コメント 0